平衡树(Splay)学习笔记

基本思想

对于二叉搜索树的每个节点，其左子树的所有节点的值都比它小，右子树的所有节点的值都比它大(当然也可以反过来)。我们可以根据这个性质进行很多操作。比如要插入一个数，则只要用当前节点的值与插入的数字比较，然后根据比较结果往下走即可。

然而如果出题人毒瘤，二叉搜索树可能会被卡成一条链，这样时间效率就会大大降低。因此就诞生了可以随时保持平衡的二叉搜索树——平衡树。

平衡树主要有权值树和区间树两种用途。权值树就是支持把数据放入删除查询之类的操作的树，类似与$STL$中的$set$那样的。区间树就是维护一个区间，且不再以节点的数据值为序来构造树，类似线段树那种。但需要注意的是，区间树的区间范围不一定是不变的，平衡树在用作区间树时是可以支持区间插值的。

平衡树有很多种，比较常用的几种之一是$Splay$。$splay$翻译过来就是”伸展”的意思，因此$Splay$又叫做伸展树。

$splay$也是伸展树的基本操作，伸展树通过$splay$来保持整体的平衡以及灵活地实现其他功能。具体功能会在接下来详细讲解。

代码结构

定义如下结构体：

1
2
3

struct splaynode {
	int data, f, son[2], size, cnt;
}splaytree[maxn];

其中$data$为节点携带的数据，$f$为节点的父亲，$son[0]$为节点左儿子，$son[1]$为节点右儿子，$size$为节点自身及其子树的节点总个数，$cnt$为节点自身的数量(即有几个与它的$data$值相同的节点)。

基础操作

判断父子关系

这个似乎不用注释。

1	int identify(int x) { return x == splaytree[splaytree[x].f].son[0] ? 0 : 1; }

连接节点

将节点$x$作为节点$fa$的子节点，做左儿子还是右儿子取决于$relation$的值。

void connect(int x, int fa, int relation) {
    if (x) splaytree[x].f = fa;
    if (fa) splaytree[fa].son[relation] = x;
}

为防止误对$0$节点进行修改，加上了判断语句。

更新节点的size值

1	void pushup(int x) { splaytree[x].size = splaytree[x].cnt + splaytree[splaytree[x].son[0]].size + splaytree[splaytree[x].son[1]].size; }

旋转节点

实际上就是把节点旋转到父节点的位置。

void rotate(int x) {
    int fa = splaytree[x].f, relation = identify(x);
    connect(splaytree[x].son[relation ^ 1], fa, relation);
    connect(x, splaytree[fa].f, identify(fa));
    connect(fa, x, relation ^ 1);
    pushup(fa), pushup(x);
}

这里在理解上可能会有点困难。我们做了三次连接:

为了方便讲解，我们假设$x$是$fa$的左儿子。当$x$是$fa$的右儿子时只是它的对称情况，实质相同。
第一次是把大小处于$x$与$fa$之间的那个节点，即$splaytree[x].son[relation \^ 1]$作为$fa$的子节点。由于$x$是$fa$的左节点，则这个节点就是$x$的右节点。设$x$节点的$data$值为$a$，这个节点为$b$，$fa$为$c$，则$a < b$。同时由于$x$是$fa$的左节点，$x$及其所有子树的节点的值都小于$c$，即$a < c$且$b < c$。综上所述，$a < b < c$。所以根据二叉搜索树的性质，这个节点在旋转后应该作为$fa$的左儿子。relation ^ 1即把relation取反。
第二次是把$x$作为其爷爷的子节点，代替$fa$。
第三次是把$fa$作为$x$的子节点。

经过这三次的连接，一个旋转操作就完成了。旋转后，节点的$size$信息需要重新统计，即使用pushup()。注意pushup()的使用顺序，否则会导致错误。

伸展操作

$Splay$专有操作，作用是把某个节点上升到指定位置，同时调整树的平衡性。

void splay(int x, int goal = 0) {
    while (splaytree[x].f != goal) {
        int fa = splaytree[x].f;
        if (splaytree[fa].f == goal) rotate(x);
        else if (identify(x) == identify(fa)) rotate(fa), rotate(x);
        else rotate(x), rotate(x);
    }
    if (!goal) root = x;
}

其中$goal$为目标位置，若不填，则默认上升到根节点。$root$为当前平衡树的根节点。

需要注意的是，为了保证树的平衡，如果当前节点与父节点、爷爷节点”三点共线”，则需要首先旋转父节点，把这三个点组成的一条链拆开，否则一个个三点组成的链连接在一起时，树的平衡就难以保证。

另外，这三个判断语句的顺序也要讲究，因为如果先判断identify(x) == identify(fa)，则当$fa$为根节点时会被判定为$0$号节点的左儿子，从而影响判断。

这里有张来自别人的图，演示了$splay$操作的具体过程:

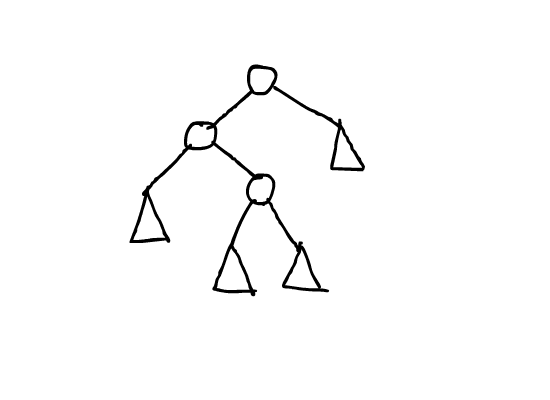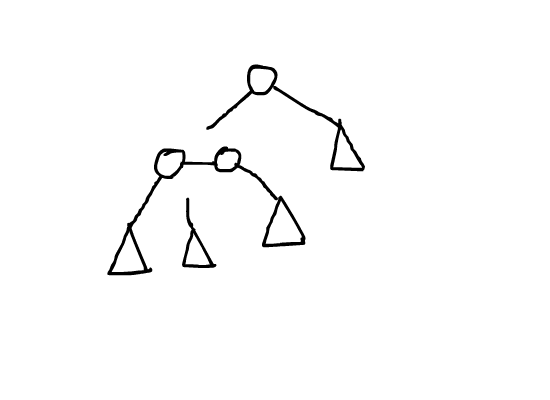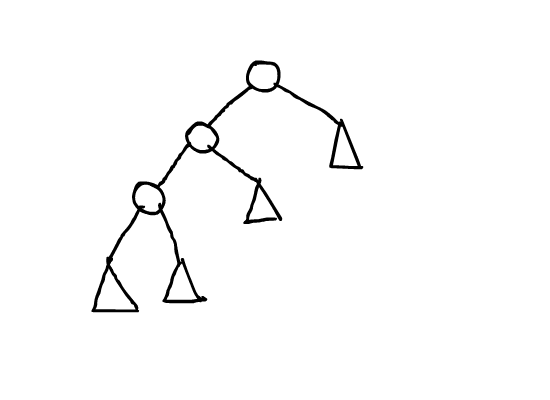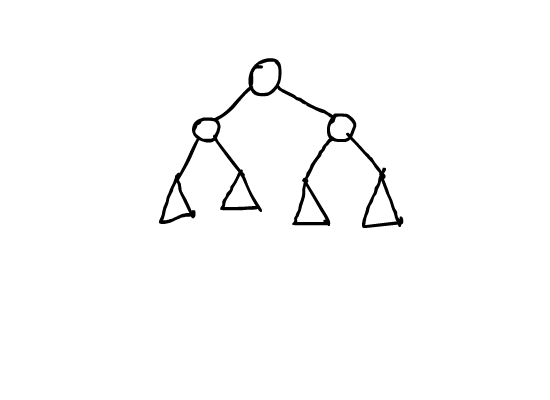
寻找节点

将值$\le v$的最大节点伸展到根节点的位置。

void find(int v) {
    int x = root;
    while (splaytree[x].data != v && splaytree[x].son[v < splaytree[x].data ? 0 : 1])
        x = splaytree[x].son[v < splaytree[x].data ? 0 : 1];
    splay(x);
}

插入节点

插入一个值为$v$的节点，并将其伸展到根节点的位置。

void insert(int v) {
    int x = root, fa = 0;
    while (x && v != splaytree[x].data) {
        fa = x;
        x = splaytree[x].son[v < splaytree[x].data ? 0 : 1];
    }
    if (x) splaytree[x].cnt++;
    else {
        x = ++cnt;
        splaytree[x].data = v;
        splaytree[x].size = splaytree[x].cnt = 1;
        splaytree[x].f = fa;
        if (fa) splaytree[fa].son[v < splaytree[fa].data ? 0 : 1] = x;
    }
    splay(x);
}

求前驱

前驱指的是小于某数的数中最大的那一个。

int pre(int v) {
    find(v);
    if (splaytree[root].data < v) return root;
    int x = splaytree[root].son[0];
    while (splaytree[x].son[1]) x = splaytree[x].son[1];
    return x;
}

求后继

后继指的是大于某数的数中最小的那一个。

int suffix(int v) {
    find(v);
    if (splaytree[root].data > v) return root;
    int x = splaytree[root].son[1];
    while (splaytree[x].son[0]) x = splaytree[x].son[0];
    return x;
}

删除节点

将待删除节点的前驱和后继分别$splay$至树根和树根右儿子的位置，则待删除节点就位于后继节点的左儿子处，且没有子节点，因此可以直接删除。

inline void clear(int x) {             //用于清除节点数据。也可以不用
    splaynode &a = splaytree[x];
    if (a.f) splaytree[a.f].son[identify(x)] = 0;
    a.data = a.cnt = a.size = a.f = a.son[0] = a.son[1] = 0;
}
void destroy(int v) {
    if (!splaytree[root].son[0] && !splaytree[root].son[1]) {
        clear(root);
        root = 0;
        cnt = 0;
        return;
    }
    int prex = pre(v), sufx = suffix(v), x = 0;
    if (prex && sufx) splay(prex), splay(sufx, prex), x = splaytree[sufx].son[0];
    else if (prex) splay(prex), x = splaytree[prex].son[1];
    else if (sufx) splay(sufx), x = splaytree[sufx].son[0];
    if (splaytree[x].cnt > 1) splaytree[x].cnt--, splay(x);
    else clear(x), update(sufx), update(prex);
}